So of course I stumbled upon a problem, it was from the topic: Inverse Trigonometric functions, this is usually taught in 12th Grade and the thing is, when we are solving problems specifically from this topic, we usually apply the concepts and ideas that we are taught. So the problem was:

Given that:
\(\cos^{-1}{\tfrac{p}{a}} + \cos^{-1}{\tfrac{q}{b}} = \alpha\), then,
What is the value of:
\(\tfrac{p^2}{a^2} - \tfrac{2pq}{ab}\cos{\alpha} + \tfrac{q^2}{b^2}\)

So any normal person should just do some manipulations and can very easily obtain the desired result. Let us be a normal person and try to solve the problem.

Let us consider \(x = \cos^{-1}{\tfrac{p}{a}}\) and \(y = \cos^{-1}{\tfrac{q}{b}}\);

Then we have,
\(\cos{(x+y) = \cos{\alpha}}\)
\(\implies \tfrac{pq}{ab} - \sin{x}sin{y} = \cos{\alpha}\)
\(\implies \tfrac{pq}{ab} - \sqrt{(1 - \tfrac{p^2}{a^2})(1 - \tfrac{q^2}{b^2})} = \cos{\alpha}\)
\(\implies (\tfrac{pq}{ab} - \cos{\alpha})^2 = (1 - \tfrac{p^2}{a^2})(1 - \tfrac{q^2}{b^2})\)

\(\implies \tfrac{p^2}{a^2} - \tfrac{2pq}{ab}\cos{\alpha} + \tfrac{q^2}{b^2} = 1 - cos^2{\alpha}\)

Hence we finally have:

\(\tfrac{p^2}{a^2} - \tfrac{2pq}{ab}\cos{\alpha} + \tfrac{q^2}{b^2} = \sin^2{\alpha}\)

Okay so this was pretty easy, but when you have checkmate in 1, you should find checkmate in 3.
So let us solve this problem using a bit of geometry.

• Step 1: Geometric interpretation

Let us consider \(x = \cos^{-1}{\tfrac{p}{a}}\) and \(y = \cos^{-1}{\tfrac{q}{b}}\);
Then we can to the above equation, draw the following figure:



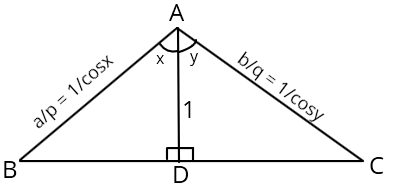
Now what we have to find is:

\(\tfrac{p^2}{a^2} - \tfrac{2pq}{ab}\cos{\alpha} + \tfrac{q^2}{b^2}\)

And this seems similar to the cosine law right?
So what should we do from the above expression is to draw another triangle!

Consider a triangle with two side lengths being: \(\tfrac{p}{a}\) and \(\tfrac{q}{b}\)
and the angle between them being \(\alpha\)

So what we essentially have to do is, try to find the third side of the following triangle!

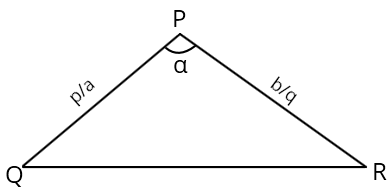
• Step 2: Similarity of Triangles

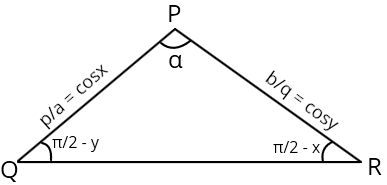
Observe that in \(\Delta PQR\), the side \(PQ = \cos{x}\) and the side \(PR = \cos{y}\)
and in \(\Delta ABC\), \(\angle BAC = x + y = \alpha\) and \(AB = \tfrac{1}{cos{x}}\) and \(AC = \tfrac{1}{cos{y}}\)

So we observe that:
\(\tfrac{AB}{PR} = \tfrac{AC}{PQ}\) and \(\angle BAC = \angle RPQ\)

Thus we have, \(\Delta ABC \sim \Delta PRQ\)

Hence the corresponding angles must be equal!
\(\angle Q = \angle C = \tfrac{\pi}{2} - y\) and \(\angle R = \angle C = \tfrac{\pi}{2} - x\)

So we have the following figure:

• Step 3: Sine and Cosine law

Now we can apply Sine rule in \(\Delta PQR\) to obtain:

\(\tfrac{QR}{\sin{\alpha}} = \tfrac{PQ}{\sin{(\tfrac{\pi}{2} - x)}} = \tfrac{\cos{x}}{\cos{x}} = 1\)

Hence we have:
\(QR = \sin{\alpha}\)

And finally, we can apply Cosine law to obtain:

\(\tfrac{p^2}{a^2} - \tfrac{2pq}{ab}\cos{\alpha} + \tfrac{q^2}{b^2} = \sin^2{\alpha}\)


I personally liked this solution because it keeps things very simplistic and we are able to use various concepts.
This is also simplistic because essentially we are working with triangles! And what the question asked helped us construct another triangle which turned out to be similar to the first one.

So what I learnt is that, when dealing with trigonometry or algebra, there are many instants where we can solve the particular problem by constructing triangles, or maybe other polygons (I haven't encountered such a problem yet). Now at the end, I still ended up using trigonometry as, I used sine rule, but things were still simple! I am hoping to find more problems which require geometric interpretation, and will be posting about the same!